ahp applications
In this section we shall skim through some applications to show their vast range and hopefully whet the readers’ appetite for the AHP, whose full potential has not been revealed yet. Nowadays, applications are so many that no survey can be comprehensive enough. However, albeit not recent, the surveys by Golden et al. [64], Zahedi [140], and Vargas [129] remain the best reference points.
City Evaluation and Planning
City Evaluation and Planning Saaty [102] proposed to use the AHP to rank a set of cities from the most to the least livable. In his study, he considered a set of cities in the United States. Indeed, the satisfaction of the final goal ‘livability’ can be decomposed into the satisfaction of some criteria, such as ‘environment’, ‘services’, ‘security’, and each of these criteria can itself be decomposed into subcriteria. For instance, the ‘services’ criterion might depend on subcriteria such as ‘transportation facilities’, ‘health care’, and so forth. Some cities are undoubtedly more livable than others. Interestingly, in this application, the AHP questionnaire was given to six decision makers representing different demographic groups and light was shed on differences of preferences between them. The research concluded presenting some conjectures on the reasons behind these discrepancies. Another innovative application was proposed by Saaty and Sagir [111]. By looking at metropolitan areas, the authors were able to classify most of the world cities into one category, out of seven, each representing an alternative model of developing a city. Some alternatives were: compact, 3-dimensional (New York City), flat (Riyadh). The AHP was used to systematically take into account good and bad points of each type of city by means of an AHP-based cost-benefit analysis.
Country Ranking
Until the late Eighties, ranking of countries was based exclusively on their gross domestic product per capita , or at least that was the most significant measure. More recently, starting in the early Nineties, a more inclusive and composite measure accounting for multiple criteria called Human Development Index has been popularized by economists such as the Nobel laureate Amartya Sen [4]. Few know that, in 1987, the AHP was already proposed to rank countries taking into account multiple criteria [95]. Clearly, in this study, the alternatives were the countries themselves, and the criteria simply all those characteristics which could make one country better than another. Indeed, with a suitable choice of criteria, this use of the AHP can be seen as a primer in the multivariate ranking of countries.
With the widespread use of (smart) mobile devices, mobile services and applications are becoming more and more successful and part of end-users’ everyday life, but why are some devices and services successful while others are not? It is indeed of great importance to identify and understand critical success factors driving the acceptance and adoption of mobile devices and different mobile services. Traditional models mainly consider a limited set of adoption factors, focusing on the perceived values of mobile services (usefulness, ease of use, cost). Nikou and Mezei [90] proposed to use the AHP to determine the most important decision criteria driving the customers’ adoption of mobile devices and mobile services. The main attributes considered include payment mode, functionality, added value, perceived quality, cost, and performance. The results of this type of studies can be essential for various service providers (operators, mobile handset manufacturers) to design profitable applications that generate value for the end-users.
Organ Transplant
It is a fact that there are more people needing human organ transplants than available organs, and that different allocations of organs can make the difference between death and life. Some combinatorial optimization problems have been proposed to match donors with organs in the best possible way, and to be fair, such algorithms account for the fact that some patients require an organ in a shorter time than others. In a study, Lin and Harris [83] proposed to use the AHP to decompose the four criteria ‘urgency’, ‘efficiency’, ‘benefit’, and ‘equity’ into subcriteria and eventually estimate their importance in the donors-organs matching process. Patients were treated as alternatives, but it is clear that their huge amount would havemade the use of subjective judgments impossible. Fortunately, in this case, the pairwise comparison matrices at the alternative level were filled automatically since different criteria were quite easily quantifiable. For instance, if the life expectancies of two patients are 1 and 2 years, it can be automatically derived that under that criterion, the first patient is two times more ‘urgent’ than the second.
Chess Prediction
The AHP has been used for forecasting too. In sports, athletes can be seen as alternatives and their characteristics as criteria, and the player rated the highest shall be regarded as the most likely to win. Here we refer to an application of the AHP for the prediction of winners in chess matches—The AHP was used to evaluate the outcome of the Chess World Championships [116] as well as of the matches between Fischer and Spassky in 1972 and Karpov and Korchnoi in 1978 [114]. A possible hierarchy for this problem is represented in Fig. 1. It is interesting to see that the values of the weights w1, . . . ,wn in this sort of problems about forecasting can be interpreted as subjective probabilities [136]. For example, in this case, w1 and w2 could be interpreted as the subjective probabilities of the victories of the two chess players.
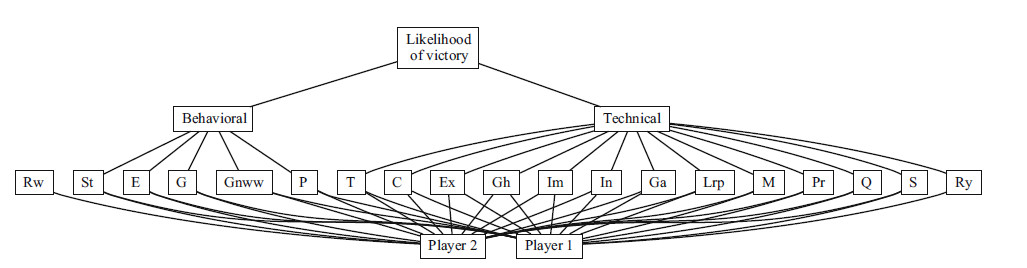
Fig. 1: A hierarchy for the chess competition problem. Abbreviations are as follows: Gamesmanship (G), Good Nerves and Will to Win (GN), Personality (P), Stamina (ST), Ego (E), Calculation (Q), Experience (EX), Good Health (GH), Imagination (IM), Intuition (IN), Game Aggressiveness (GA), Long Range Planning (LRP), Memory (M), Preparation (PR), Quickness (Q), Relative Youth (RY), Seconds (S), Technique (M). For a fuller description see the original paper [116]
Facility Location
In Turku, a city in the South-West of Finland, the AHP has been used to find the best location the new ice hockey stadium (nowcalled Turku Arena). Several criteria were used to evaluate different locations. Among the criteria one can find the accessibility of the arena, the possibility of having car parking, the quality of the soil on which the arena shall be built, and so forth. Carlsson andWalden [34] gave a frank political account of the decision process, which involved the local administration, and whose selected alternative was the third best ranked, and not the
Ref:
- L. G. Vargas. An overview of the analytic hierarchy process and its applications. European Journal of Operational Research, 48(1):2–8, 1990.
- F. Zahedi. The analytic hierarchy process—A survey of the method and its applications. Interfaces, 16(4):96–108, 1986.
- T. L. Saaty. Absolute and relative measurement with the AHP. The most livable cities in the United States. Socio-Economic Planning Sciences, 20(6):327–331, 1986.
- T. L. Saaty and M. Sagir. Global awareness, future city design and decision making. Journal of Systems Science and Systems Engineering, 21(3):337–355, 2012.
- K. Peniwati and T. Hsiao. Ranking countries according to economics, social and political indicators. Mathematical Modelling, 9(3-5):203–209, 1987.
- S. Anand and A. Sen. Human development index: methodology and measurement. Technical report, Human Development Report Office (HDRO), United Nations Development Programme (UNDP), 1994.
- C. S. Lin and S. L. Harris. A unified framework for the prioritization of organ transplant patients: Analytic hierarchy process, sensitivity and multifactor robustness study. Journal of Multi-Criteria Decision Analysis, 20(3-4):157–172, 2013.
- S. Nikou and J. Mezei. Evaluation of mobile services and substantial adoption factors with analytic hierarchy process (AHP). Telecommunications Policy, 37(10):915–929, 2013.
- T. L. Saaty and L. G. Vargas. Hierarchical analysis of behavior in competition: Prediction in chess. Systems Research and Behavioral Science, 25(3):180–191, 1980.
- T. L. Saaty and L. G. Vargas. Modeling behavior in competition: The analytic hierarchy process. Applied Mathematics and Computation, 16(1):49–92, 1985.
- R. R. Yager. An eigenvalue method of obtaining subjective probabilities. Systems Research and Behavioral Science, 24(6):382–387, 1979.
- C. Carlsson and P. Walden. AHP in political group decisions: A study in the art of possibilities. Interfaces, 25(4):14–29, 1995.
