Fuzzy AHP (chang) steps

Step1.The fuzzy synthetic extent value (Si) with respect to the ith criterion is defined as equation 1 .

To obtain equation 2;

perform the “fuzzy addition operation” of m extent analysis values for a particular matrix given in equation 3 below, at the end step of calculation, new (l, m, u) set is obtained and used for the next:

Where l is the lower limit value, m is the most promising value and u is the upper limit value.
and to obtain equation 4;

perform the “fuzzy addition operation” of       values give as equation 5:

and then compute the inverse of the vector in the equation (5) equation (6) is then obtained such that

Step 2. The degree of possibility of

is defined as equation 7: 

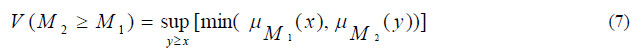
and x and y are the values on the axis of membership function of each criterion. This expression can be equivalently written as given in equation 8 below:

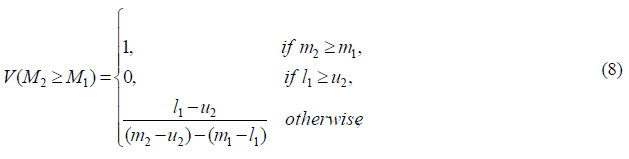
where d is the highest intersection point  and  (see Figure 1)

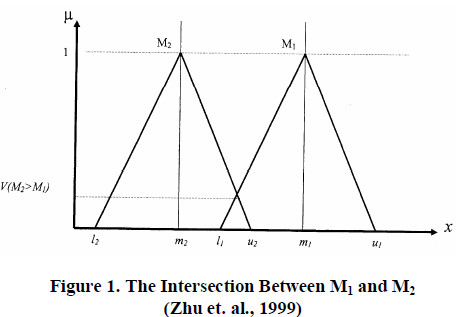
To compare M1 and M2; we need both the values of V(M2≥ M1) and V(M1≥M2):

Step 3. The degree possibility for a convex fuzzy number to be greater than k convex fuzzy numbers

can be defined by

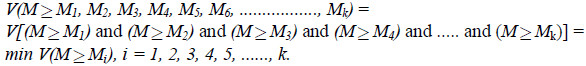
Assume that equation 9 is

For k = 1, 2, 3, 4, 5, ……, n; k ≠ i. Then the weight vector is given by equation 10:

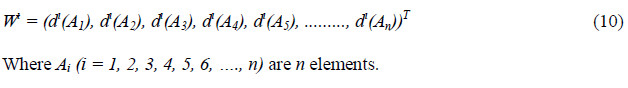
Step 4. Via normalization, the normalized weight vectors are given in equation 11:

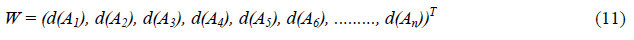
Where W is non-fuzzy numbers.

Chang, D. Y., (1992), “Extent Analysis and Synthetic Decision”, Optimization Techniques and Applications, World Scientific, Singapore, 1, 352.

Zhu, K. J., Jing, Y., and Chang, D. Y., (1999), “A Discussion on Extent Analysis Method and Applications of Fuzzy-AHP”, European Journal of Operational Research, 116, 450-456.