Gogus and Boucher (1998) developed a method for calculating the inconsistency ratio of fuzzy pairwise comparison matrices, which its steps are given as follows.
STEP 1: Transform a triangular fuzzy matrix into two independent matrices. At this step, a triangular fuzzy matrix is divided into two matrices, assuming that the triangular fuzzy number is presented as follows.
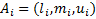
Then, we will get,
The first matrix can be created by middle numbers of the triangular fuzzy matrix, that is:
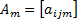
The second matrix can be created by the geometric mean (GM) of the upper and lower bounds of the triangular fuzzy matrix, that is:
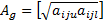
STEP 2: Compute the weight vector based on the saaty method and calculation of lamda(max)
STEP 3: Calculate the consistency index (CI): for each matrix, the CI can be calculated based on the following equation:
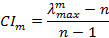
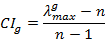
STEP 4: Calculate the consistency ratio (CR) of the matrices in Problem. In order to compute the CR, the consistency index (CI) of each matrix is divided by its random index (RI).
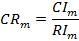
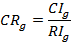
If the values of CRm and CRg are less than 0.1, the matrices are consistent.
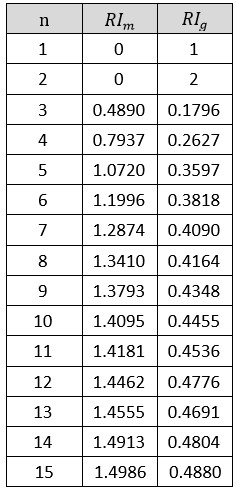
The values of the RI given by Gogus and Boucher method are different from those in the saaty method. Gogus and Boucher redeveloped the random indices (RI) Table for fuzzy pairwise comparison matrices with creating 400 random matrices. The following table presents the values of the RI for each matrix of Gogus and Boucher method.
hi
if n is 23 . what is the values of the RI ? I need its formula
Its like you read my mind! You seem to know so much about this, like
you wrote the book in it or something. I think that you could do with some pics
to drive the message home a little bit, but other than that, this
is wonderful blog. A fantastic read. I’ll definitely be back.
Any example of applying the method, please?
MCDM METHODS
Thanks for taking the time to talk about this, I feel strongly about it and enjoy studying more on this topic. If possible, as you acquire experience, would you mind updating your weblog with far more data? Its very helpful for me.
Took me time to read all the comments, however I really loved the article. It proved to be very useful to me and Im positive to all of the commenters here! Its all the time good when you cant only learn, but in addition engaged! I am certain you had joy penning this article. Anyway, in my language, there arent much good source like this.
May I reference part of this on my blog if I include a link to this webpage?
I am unquestionably bookmarking this web site and sharing it with my friends. You will be getting plenty of visitors to your web site from me!
I love the theme youre using in your blog Im so grateful with this post and thank you a lot for sharing it with us. Will definately keep close track of these pages.
hello
Can you explain more for step2؟
i have checked this site a few times now and i have to say that i find it quite exeptional actually. keep it up!
Thanks for the marvelous posting! I genuinely enjoyed reading it, you
might be a great author. I will be sure to bookmark your
blog and will often come back from now on. I want to encourage that you
continue your great writing, have a nice evening!