The steps of the fuzzy AHP technique using Chang’s method can be given as follows:

STEP 1: Draw the hierarchical chart

STEP 2: Define fuzzy numbers for performing the pair-wise comparisons

STEP 3: Create the pair-wise comparison matrix  using fuzzy numbers

The pair-wise comparison matrix can be expressed as follows:

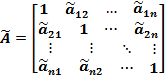
If there are several experts, elements of a complete pairwise comparison matrix used in the fuzzy AHP method is a triangular fuzzy number where the first component (l) is the least comments, the second component (m) is the mean of numbers and the third component (u) is the maximum number.

STEP 4: Calculate 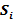  for each row of the pair-wise comparison matrix

 can be calculated using the following formula:

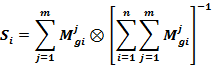
Where i represents the row number and j denotes the column number. In the formula,  is triangular fuzzy numbers of pairwise comparison matrices. The values of   and can be calculated by using the following formulas, respectively:

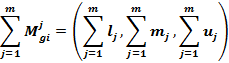
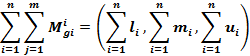
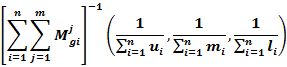
In the above formulas,,  and  are the first, second, and third components of the fuzzy numbers, respectively.

STEP 5: Compute the magnitude of  with respect to each other

In general, if  and  are two triangular fuzzy numbers, then, as shown in the following figure, the magnitude of  with respect to   can be defined as follows:

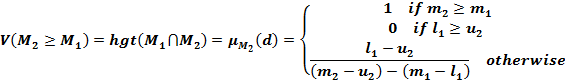
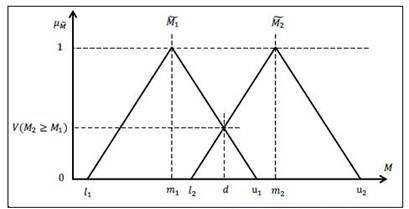
On the other hand, the magnitude of a triangular fuzzy number from k as another triangular fuzzy number can be obtained by the following formula:

STEP 6: Compute the weight of the criteria and alternatives in the pair-wise comparison matrix

The following formula can be used for this purpose:

Therefore, the  unnormalized weight vector can be given as follows:

STEP 7: Calculate the final weight vector

To calculate the final weight  vector, the calculated weight vector in the previous step should be normalized, then :