### Step 1: Define the Problem and the Goal
Start by defining the overall goal of the decision. This goal is broken down into a hierarchy of criteria and sub-criteria. Finally, alternatives (choices) are listed at the bottom of the hierarchy.
### Step 2: Establish Pairwise Comparison Matrices
For each criterion and sub-criterion, a **pairwise comparison matrix** is formed to compare the relative importance of each element. The matrix is square and its size depends on the number of elements being compared. For example, if there are \( n \) criteria, the matrix \( A \) is of size \( n \times n \), where each entry represents a comparison between two criteria.
The matrix \( A \) is given as follows:
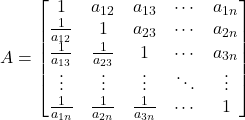
Each element \( a_{ij} \) represents the relative importance of criterion \( i \) compared to criterion \( j \), where:
– \( a_{ij} = 1 \) if criteria \( i \) and \( j \) are equally important.
– \( a_{ij} > 1 \) if criterion \( i \) is more important than criterion \( j \).
– \( a_{ij} < 1 \) if criterion \( j \) is more important than criterion \( i \).
### Step 3: Calculate the Priority Vector
The **priority vector** (also called the eigenvector) represents the relative weights of the elements. It is derived by normalizing the pairwise comparison matrix. One common method is to calculate the geometric mean of each row, and then normalize the vector so that the sum of its elements is 1.
To compute the priority vector \( w \), follow these steps:
1. **Compute the geometric mean** of each row:
![]()
2. **Normalize the vector** by dividing each element by the sum of all elements:
![]()
This gives the priority vector \( w \), which represents the weights of the criteria.
### Step 4: Check for Consistency
The **Consistency Ratio (CR)** measures how consistent the judgments are. A perfectly consistent matrix satisfies \( a_{ij} \cdot a_{jk} = a_{ik} \). In practice, some inconsistency is allowed. The consistency check involves the following steps:
1. Compute the **weighted sum vector**:
![]()
Where \( A \) is the pairwise comparison matrix, \( w \) is the priority vector, and \( \lambda_{\text{max}} \) is the largest eigenvalue of the matrix.
2. Compute the **Consistency Index (CI)**:
![]()
Where \( n \) is the size of the matrix.
3. Compute the **Consistency Ratio (CR)**:
![]()
Where \( RI \) is the **Random Index**, which depends on \( n \) (the number of elements). If \( CR \leq 0.1 \), the level of inconsistency is acceptable.
### Step 5: Aggregate the Results
After determining the priority vectors for all levels of the hierarchy, combine the results to determine the final decision by calculating the overall score for each alternative. This is done by multiplying the weights of the criteria by the weights of the alternatives under each criterion and summing the results.
![]()
Where:
– \( w_j \) is the weight of criterion \( j \),
– \( v_{ij} \) is the score of alternative \( i \) with respect to criterion \( j \).
The alternative with the highest score is the most preferred option.
### Summary of Steps:
1. Define the goal and build the decision hierarchy.
2. Construct pairwise comparison matrices for each level.
3. Calculate priority vectors by normalizing the matrices.
4. Check for consistency using the Consistency Ratio.
5. Aggregate the priorities to rank the alternatives.
These steps form the core of the AHP process with the help of the relevant formulas.

Recent Comments